Just how likely is it that Governor Robert Bentley had an affiar with his top official?
I've lived in Alabama since December 2015.
In recent Alabama news, Governor Robert Bentley has been accused of wrongly dismissing his top law enforcement official. The official says that Bentley asked him to lie to the district attorney about a corruption case involving House Speaker Mike Hubbard. The ex-law enforcement official says he refused to lie and was terminated by Bentley.
The official, Spencer Collier, also revealed to the media that he'd discovered a sexual text message between Bentley and his top official (a woman). Bentley has denied having a physical affair with his official Rebekah Mason.
So, why am I writing about this?
I think this is a nice opportunity to utilize Bayes' Theorem to estimate the chance that Bentley really did have an affair. I'm going to keep this short and simple.
Let A be the event that Bentley had an affair with Rebekah Mason.
Let B be the event that this recording is revealed to the press and that Robert Bentley does not deny that the conversation in the recording was between him and Rebekah Mason.
Now, we are looking to estimate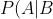) .
.
We'll use Bayes' Theorem:
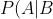&space;=&space;\frac{P(B|A)P(A)}{P(B|A)P(A)&space;+&space;P(B|A^{C})P(A^C)})
Now, this is the fun part. We need to estimate three different probabilities.
1. P(B|A) - the probability that this recording would be revealed to the press given that he actually had an affair.
Imagine a world where Bentley is having an affair with Mason. What are the chances that this recording gets revealed to the press? Apparently Bentley was doing some things that upset some people. So there's motive. The recording must've been tough to actually get. It's tough to estimate how difficult it was to actually get but you'd think Bentley would be trying to keep the affair a secret. So for this recording to be revealed to the press given that he is having an affair, someone who has been wronged by Bentley must know of the affair and plant a recording device to try and catch him (I'm presuming this is how it happened) and then actually reveal it to the press. This seems like it's a pretty unlikely scenario. Let's say 25%.
2. P(A) - the prior. The probability that Bentley had an affair with Rebekah Mason before the recording was released.
Let's start with a general fact. About 25% of men cheat on their wives. Let's say Bentley's average for now. He has about 75 women in his life lets say but lets say Rebekah is the closest and thus the most likely to be a mistress. So lets say that leaves us at about 4% that they were sleeping together.
Now consider that Rebekah is attractive (she's a former beauty queen) and that they have a long and close relationship (she has said to influence his decision making a lot). Let's say that puts us at about 6%. Now, one more piece of information. Bentley got divorced at the end of last year. Let's say that puts us at 10%.
3. P(B|A*) - the probability that this recording is revealed given that Bentley did not have an affair.
Now, this is where things get a little tricky for Bentley's side of the story. Imagine a world where Bentley has never had a sexual relationship with Mason. What are the odds of a recording like this being revealed to the media and Bentley not denying that the conversation was between him and Mason given the fact that they were not having an affair? The nature of the conversation indicates there was a high probability that they had been intimate with each other if in fact it was Mason on the other end of the line. Now Bentley has not denied that he was talking to Mason in the recording. That's included in event B. He acknowledged this conversation was between him and Mason and apologized for it. I reckon that the probability that this tape is revealed and that he acknowledges it given that they haven't had an affair is about .01.
I feel like I've done an honest job at estimating these probabilities. Let's plug in the numbers to Bayes' theorem and see what we come up with.
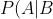&space;=&space;\frac{P(B|A)P(A)}{P(B|A)P(A)&space;+&space;P(B|A^{C})P(A^C)}&space;=&space;\frac{.25*.10}{.25*.10+.01*.90} = .74)
So according to this analysis there's a 74% chance that Bentley and Mason had an affair.
In recent Alabama news, Governor Robert Bentley has been accused of wrongly dismissing his top law enforcement official. The official says that Bentley asked him to lie to the district attorney about a corruption case involving House Speaker Mike Hubbard. The ex-law enforcement official says he refused to lie and was terminated by Bentley.
The official, Spencer Collier, also revealed to the media that he'd discovered a sexual text message between Bentley and his top official (a woman). Bentley has denied having a physical affair with his official Rebekah Mason.
So, why am I writing about this?
I think this is a nice opportunity to utilize Bayes' Theorem to estimate the chance that Bentley really did have an affair. I'm going to keep this short and simple.
Let A be the event that Bentley had an affair with Rebekah Mason.
Let B be the event that this recording is revealed to the press and that Robert Bentley does not deny that the conversation in the recording was between him and Rebekah Mason.
Now, we are looking to estimate
We'll use Bayes' Theorem:
Now, this is the fun part. We need to estimate three different probabilities.
1. P(B|A) - the probability that this recording would be revealed to the press given that he actually had an affair.
Imagine a world where Bentley is having an affair with Mason. What are the chances that this recording gets revealed to the press? Apparently Bentley was doing some things that upset some people. So there's motive. The recording must've been tough to actually get. It's tough to estimate how difficult it was to actually get but you'd think Bentley would be trying to keep the affair a secret. So for this recording to be revealed to the press given that he is having an affair, someone who has been wronged by Bentley must know of the affair and plant a recording device to try and catch him (I'm presuming this is how it happened) and then actually reveal it to the press. This seems like it's a pretty unlikely scenario. Let's say 25%.
2. P(A) - the prior. The probability that Bentley had an affair with Rebekah Mason before the recording was released.
Let's start with a general fact. About 25% of men cheat on their wives. Let's say Bentley's average for now. He has about 75 women in his life lets say but lets say Rebekah is the closest and thus the most likely to be a mistress. So lets say that leaves us at about 4% that they were sleeping together.
Now consider that Rebekah is attractive (she's a former beauty queen) and that they have a long and close relationship (she has said to influence his decision making a lot). Let's say that puts us at about 6%. Now, one more piece of information. Bentley got divorced at the end of last year. Let's say that puts us at 10%.
3. P(B|A*) - the probability that this recording is revealed given that Bentley did not have an affair.
Now, this is where things get a little tricky for Bentley's side of the story. Imagine a world where Bentley has never had a sexual relationship with Mason. What are the odds of a recording like this being revealed to the media and Bentley not denying that the conversation was between him and Mason given the fact that they were not having an affair? The nature of the conversation indicates there was a high probability that they had been intimate with each other if in fact it was Mason on the other end of the line. Now Bentley has not denied that he was talking to Mason in the recording. That's included in event B. He acknowledged this conversation was between him and Mason and apologized for it. I reckon that the probability that this tape is revealed and that he acknowledges it given that they haven't had an affair is about .01.
I feel like I've done an honest job at estimating these probabilities. Let's plug in the numbers to Bayes' theorem and see what we come up with.
So according to this analysis there's a 74% chance that Bentley and Mason had an affair.
Written on April 21, 2016